https://doi.org/10.34024/prometeica.2024.31.19568
TEACHING AND LEARNING MATHEMATICS FOR THE PLANET AND EACH OTHER
DIÁLOGO, RESPONSABILIDADE E EDUCAÇÃO MATEMÁTICA
Ensinar e aprender matemática para o planeta e para os outros
DIÁLOGO, RESPONSABILIDAD Y EDUCACIÓN MATEMÁTICA
Enseñar y aprender matemáticas para el planeta y para los demás
Richard Barwell
(University of Ottawa, Canada)
richard.barwell@uottawa.ca
Recibido: 01/10/2024
Aprobado: 12/11/2024
RESUMO
O mundo está em dificuldades e a matemática está envolvida. Somos educadores de matemática - professores, pesquisadores, ativistas. Qual é a nossa resposta? Qual é a nossa responsabilidade? Na primeira parte deste texto, sintetizo as características da educação matemática de que podemos precisar: responsabilidade, crítica, imaginação, incerteza, conduzida em um espírito de relacionamento ético, humildade, liberdade de aprendizado e reconhecimento do valor fundamental de cada ser humano, criatura não humana, idioma, cultura e ecossistema, e nossa dependência deles para nossa própria existência e sobrevivência. Na segunda parte, proponho o dialogismo como uma postura epistemológica para a educação matemática da qual essas características decorrem. Desenvolvo alguns dos fundamentos epistemológicos do dialogismo, baseando-me particularmente no trabalho de Bakhtin sobre a linguagem e sua filosofia do ato. Essas ideias incluem significado, resposta, capacidade de resposta, interdependência e não-finalidade. Ilustro essas ideias em relação a duas situações: linguagem e diversidade cultural nas salas de aula de matemática; e o papel da matemática no contexto da biodiversidade. Concluo enfatizando que pensar dialogicamente sobre a matemática em uma época de problemas aponta para a importância de nossa responsabilidade uns com os outros em cada momento de nossa existência.
Palavras-chave: educação matemática. ecossistema. diálogo. responsabilidade.
ABSTRACT
The world is in trouble and mathematics is involved. We are mathematics educators— teachers, researchers, activists. What is our response? What is our responsibility? In the first part of this text, I engage with selected contributions to MES to synthesise features of the mathematics education we might need: responsibility, critique, imagination, uncertainty, conducted in a spirit of ethical relationality, humility, freedom of learning, and a recognition of the fundamental worth of every human being, non-human creature, language, culture and ecosystem, and our dependence on them for our own existence and survival. In the second part, I propose dialogism as one epistemological stance for mathematics education from
which these features follow. I develop some of the epistemological foundations of dialogism, drawing particularly on Bakhtin’s work on language and his philosophy of the act. These ideas include meaning, response, answerability, interdependence and non-finality. I illustrate these ideas in relation to two situations: language and cultural diversity in mathematics classrooms; and the role of mathematics in the context of biodiversity. I conclude by emphasising that thinking dialogically about mathematics in a time of trouble points to the importance of our responsibility to each other at each moment of our existence.
Keywords: mathematics education. ecosystem. dialogue. responsibility.
RESUMEN
El mundo está en dificultades y las matemáticas están implicadas. Somos educadores matemáticos: profesores, investigadores, activistas. ¿Cuál es nuestra respuesta? ¿Cuál es nuestra responsabilidad? En la primera parte de este texto, sintetizo las características de la educación matemática que podríamos necesitar: responsabilidad, crítica, imaginación, incertidumbre, llevada a cabo en un espíritu de relacionalidad ética, humildad, libertad de aprendizaje y reconocimiento del valor fundamental de cada ser humano, criatura no humana, lengua, cultura y ecosistema, y de nuestra dependencia de ellos para nuestra propia existencia y supervivencia. En la segunda parte, propongo el dialogismo como una postura epistemológica para la educación matemática de la que se derivan estas características. Desarrollo algunos de los fundamentos epistemológicos del dialogismo, basándome especialmente en la obra de Bajtin sobre el lenguaje y su filosofía del acto. Estas ideas incluyen el significado, la respuesta, la capacidad de respuesta, la interdependencia y la no finalidad. Ilustro estas ideas en relación con dos situaciones: el lenguaje y la diversidad cultural en las aulas de matemáticas; y el papel de las matemáticas en el contexto de la biodiversidad. Concluyo subrayando que pensar dialógicamente sobre las matemáticas en una época de problemas apunta a la importancia de nuestra responsabilidad mutua en cada momento de nuestra existencia.
Palabras clave: educación matemática. ecosistema. diálogo. responsabilidad.
Are you worried? Do you know that the world is in trouble? Here are some of the things that I think are big trouble: climate change; the sixth great extinction; the catastrophic loss of biodiversity; planetary- scale pollution; the mass disappearance of languages and cultures; the massive gap between rich and poor; threats to democracy by demagogues and populists; the risk of nuclear war; and the impact of all of this on all of us and, disproportionately, on poor and marginalised humans, as well as a vast number of non-human species.
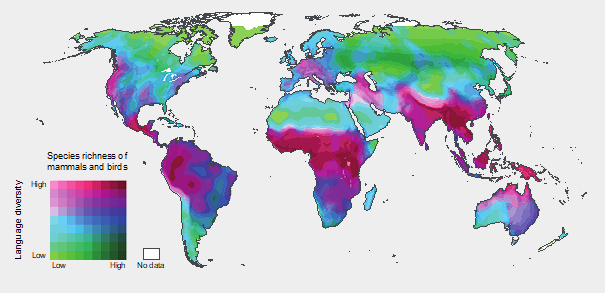
I think we mostly agree that mathematics is intimately involved in all of these problems and in multiple ways. Mathematics is an important, if imperfect, way of recognising and understanding these troubles. Without mathematics, we cannot experience global changes in the climate (although we are all increasingly experiencing local effects of global climate change); we cannot easily see global trends in language loss or income inequality; we cannot unmask the lies that undermine democracy. Mathematics helps us to describe these troubles, to project their future course under different scenarios, and to communicate about them. Here’s an example that connects two things that I have focused on in my research: language diversity and biodiversity. An analysis presented in a report of the Intergovernmental Program on Biodiversity and Ecosystem Services (IBPES, 2018) showed a spatial association between language diversity and species diversity (Figure 1). The authors took two studies, one reporting the geographical locations of the world’s languages (Hammarström, Forkel & Haspelmath, 2017) and the
other analysing the terrestrial diversity of vertebrates focusing on birds and mammals (Jenkins, Pimm & Joppa, 2013), and mapped them together.

Figure 1. Mapping language diversity and biodiversity (IPBES, 2018, p. xxxiv)
Figure 1 shows the resulting association graphically. We see that where biodiversity—the diversity of species in the local ecosystem—is high, so is language diversity and, by extension, cultural diversity. Here’s why this matters:
Land degradation negatively affects the cultural identity of some communities, particularly indigenous peoples and local communities, and erodes their traditional knowledge and management systems. An individual’s or society’s relationship to land shapes identity, traditions and values, as well as spiritual beliefs and moral frameworks […] Land degradation causes a loss of sense of place and of spiritual connection to the land, in indigenous peoples and local communities as well as in urban residents living far from the affected areas.
Alienation of indigenous peoples and local communities from the land often leads to the irreversible loss of accumulated knowledge on how to manage land. In most cases, land management practices based on indigenous and local knowledge have proven to be sustainable over long time periods and offer alternative models to the currently dominant human-nature relationship. (IPBES, 2018, pp. xxxiv–xxxv)
The first thing I want to point out is how much mathematics is embedded in this graphic, much of it in the two underlying studies that were used to produce it. Mathematics is powerful in doing this kind of work and the graphic is an example of mathematics being used to communicate this important association. The recent shifts in public understanding of climate change or about the Covid-19 pandemic depend greatly on mathematical communication. There are also hints about what mathematics cannot capture so well, such as spirituality, sense of and connection to place, and ways of living in greater harmony with the rest of nature. We can also imagine the diverse mathematical practices and ways of knowing that are present in relation to different languages and ecosystems.
The IPBES reports (e.g., 2019) make grim reading. There are pages filled with graphs, charts and diagrams showing different aspects of the catastrophe affecting our planet’s ecosystem. From oceanic pollution to overfishing, from land degradation to invasive species, from increasing urbanisation to accelerating rates of extinction, from language loss to the eradication of Indigenous cultures, it is clear that much is out of balance. Should we lose hope? What can we do? The rest of this paper is divided into two parts. The first part considers what these troubles mean for mathematics education. The second part argues for the value of a dialogic epistemological stance. In both parts, my thinking is developed in dialogue with the work of others in the MES community.
What is our responsibility as mathematics educators and mathematicians faced with these complex troubles? What is our responsibility to our students, to children, to our society and to all the creatures and organisms with whom we share our planet? The proceedings of the Mathematics Education and Society (MES) conference held in Portland, Oregan, in 2015 is framed, in the introduction, by a version of this question, stating:
Ubiratan D’Ambrosio has passionately drawn attention to the ethical responsibilities of mathematicians and mathematics educators in relation to the most important problem facing humankind, namely survival with dignity. (p. 14)
In this part of the paper, I interact with three of the plenary addresses given at that conference (which I attended). D’Ambrosio spoke more about our responsibilities. His own view of the trouble we are in was clear-eyed, but not without hope:
Putting together all the alerts and reports and the serious concerns of responsible scientific bodies, we foresee a situation of chaos, out of which we, as educators, have to evolve to a sustainable civilization, with peace in all its dimension (individual, social, environmental and military) and societies with justice and dignity for all. But mathematics curricula ignores critical issues threatening the survival of civilization. (d’Ambrosio, 2015, p. 21)
D’Ambrosio aligns himself with the idea, well-established in much ecological thought, that in every type of trouble lies an opportunity to rethink and make something better. Thus far, mathematics education has not been very attentive to the trouble we are in:
Important innovations in mathematics education are not producing significant results. National and international large scale assessments are discouraging, although we point to a few pockets of excellence. But how to reach the decision makers, that is, how to convey relevant mathematics to a large sector of society? […] We need new ideas, new approaches, to face the problems affecting the world. Our generation and our approaches are not producing the global changes to avoid total disaster. We need to allow the new generations to think in a new way […] The school must be a space not only for instruction, but primarily for socializing and for criticizing what is observed and felt in everyday life. This may stimulate creativity, leading to a new thinking. (pp. 23–24)
In sum, mathematics educators need to think and do differently. This is always challenging; D’Ambrosio warns of the “epistemological cage” of mathematics, of students learning the “mathematical games” that make up most curricula, and the absence of ethical thinking that this entails. This makes sense to me but thinking differently is not always easy. As well as our epistemological cages, we are caught in global and local structures of society (forms of reasoning, epistemologies), including various versions of capitalism that seem designed to alienate us from the relationships that we depend on for our well-being and survival. The degradation of the planet’s ecosystems is one product of this global economic system, as is the accelerating homogenisation of the world’s cultural and linguistic diversity at the expense of those who are marginalised by this system. How can we think and do differently? What are the challenges?
In the text for his address at the same conference, Skovsmose writes about critical mathematics education as a response to the troubles we face. He concentrated particularly on the relationship between critique and uncertainty:
I see critique as an expression of uncertainty. However, I do not think we should let ourselves become paralysed by this observation. I do not subscribe to any version of the following argument: since we cannot be sure that the critique is appropriate, we better do nothing. Instead we actively have to face the paradox of critique […] When I talk about critical mathematics education I also acknowledge the paradox of critique. There are simply too many critical issues related to mathematics education that are in need of being addressed. But we do not have any adequate theoretical or practical basis for ensuring any such critique can be conducted adequately. This applies when we address: social exclusion through mathematics education; unjustified trust in mathematics-based information; strategies for providing empowerment through
mathematical literacy; etc. Also critical mathematics education becomes an expression of uncertainty. (Skovsmose, 2015, p. 113)
This position is curiously reassuring. It is a bit like the idea that stupidity is doing the same thing over and over again and expecting to eventually get a different result. In some respects, mathematics curricula and mathematics teaching has been doing the same thing over and over again for centuries and the results are not any different. Better to try something different (and of course, many inspiring people have tried— I am thinking here about systems), even if we do not have certainty. The troubles we face can also be an opportunity to rethink our society and the critique in critical mathematics education can be a part of this rethinking. How can we do this as teachers and educators?
Skovsmose proposes that we need “pedagogical imagination” as an important part of critique:
Criticising something also means imagining that things could be different, because it is through a critique that one also expresses visions, hopes, and aspirations. Thus I see imaginations as a profound element of a critical activity, and imaginations carry with them a strong sense of uncertainty. (p. 113)
1
At a time of uncertainty, we may feel a lack of a firm ontological and epistemological footing (there are no universal categories). This uncertainty creates opportunities for exploitation, disinformation, populism, oppression and so on, but paradoxically, also makes space for critique and for imagining new ways to counter these forces, just as d’Ambrosio called for. For Skovsmose, critical mathematics education involves combining uncertainty, pedagogical imagination and social justice. Its purpose is critique: of mathematics, with mathematics, and of critical mathematics education itself. But Skovsmose is not naïve! Engaging in these kinds of critique and risking our pedagogical imagination may result in mistakes, dead ends, illusions that turn out to be nothing more than reassuring mirages; but if we do not imagine, we will have no chance of thinking and doing differently63F .
Something is missing though. Yes, we must recognise our responsibilities to humanity; yes, we need critique and imagination; but the troubles we face are also the product of different kinds of responsibility, critique and imagination—and mathematics. Climate change, for example, is an effect of our technological consumer capitalist society: unlimited consumption based on extraction, exploitation and colonisation, facilitated and accelerated by technology and mathematics (among other things). What is missing in my account so far is a sensitivity to our responsibilities to others, in which I include not just humans, but also societies, species and ecosystems.
In his contribution to MES in 2015, Fasheh discusses what ethical relationships in education might require to challenge some dangerous myths, such as, in particular, the myth that ‘academic’ mathematics is superior to any other kind of mathematical thinking. His ideas are always located in his own experience and language, including the Arabic from which his words come, and his life under colonisation and occupation in Palestine (of which I have no direct knowledge). In drawing on his text, I am sharing my responses to Fasheh’s words, rather than giving a definitive account of his thinking, which I think we would both agree would be impossible. In relation to the trouble we face, and the preceding discussion of responsibility, imagination and ethics, I want to highlight three “rooted words” shared by Fasheh:
Mujaawarah refers to any group of people who freely decide to meet regularly and start from the existential situation where they happen to be, with no internal or external authority, in their quest to learn, understand, and act. A basic aspect in mujaawarah is both personal and communal freedom to learn and act—in harmony with wellbeing and wisdom. (p. 48)
A person’s worth is not judged by professional committees and measurements that claim to be objective and universal, but by the five meanings embedded in the word yuhsen. The five meanings embody plurality, humility, contextual thinking, and reflection on the inter-connectedness in life. According to it, every person naturally has worth, which is incomparable with that of others’ […] Whereas a person’s worth in dominant
I feel slightly better about the many mistakes and dead-ends in my own practice and research.
practice is given by a number, one’s worth in yuhsen is given through relations and through interconnectedness of five dimensions. (p. 50)
Muthanna refers to a relation between two persons that becomes very important in the lives of both, and yet has a life of its own. It is neither legal nor intellectual nor economic nor social; it develops freely between the two. It is neither a couple nor dual— although the latter is usually used to refer to it. Muthanna does not perceive the other as non-I or as a person that is a copy of I, or a higher synthesis with I. Each person remains who s/he is, but a relation develops that becomes important to both. In this sense, it embodies a logic that is different from that of Aristotle and Hegel. It is also different from the logic of Descartes who said “I think, therefore I am.” In the logic of muthanna, “You are, therefore I am”—my existence depends on my relation with you. (p. 51)
What kind of relationships do these words suggest? What do they imply for our work as mathematics educators? For me, they bring to mind an image of mathematics education that I have rarely seen. It is an anti-oppressive mathematics education based fundamentally on “non-power” relations, in which learners come together out of mutual interest, in which each participant (learner or teacher) is deeply valued and respected for their worth, and which recognises that our own existence depends on others. Fasheh challenges us to conceive of mathematics education based on the idea that “you are, therefore I am”. It also involves not seeing mathematics as a closed field in which learners and teachers have nothing to add, but as a living domain of thinking that encompasses much more than is found in many curricula.
I also read these ideas from a broader ecological perspective. Many of the troubles that we face arise precisely because many humans judge themselves to be more valuable, to have more worth, than other species. As a species, we tend to reshape biodiverse ecosystems into monocultures because we fail to see the importance of plurality. Mathematics is often an important tool used to (try to) control ecosystems, other species, people, etc., in pursuit of profit and the comfort of a minority. Our interdependence extends to other species, many of which humans exploit or are eliminating. In doing so, we are destroying ourselves: “you are, therefore I am” also applies to other species.
Thus, the mathematics education we need might have the following features: responsibility, critique, imagination, uncertainty, conducted in a spirit of ethical relationality, including humility, freedom of learning, and a recognition of the fundamental worth of every human being, non-human creature, language, culture and ecosystem, and our dependence on them for our own existence and survival. How can we be mathematics educators like this? What does it mean to know and learn mathematics or do research in mathematics education if these are the features we seek?
The features of the mathematics education I have synthesised imply something about how we come to know mathematics. In this part of the paper, I argue that a dialogic epistemological perspective is consistent with and foundational for these principles. This perspective is one way of drawing together different aspects of the foregoing discussion; there are, of course, other possible and valuable perspectives. I will summarise some of the main assumptions of this dialogic perspective and then illustrate how they apply in some different situations.
What is dialogue? What does it mean to you? My own thinking about dialogue has developed through reading Bakhtin’s work, which I first read more than twenty years ago but which I am still working to understand. The more I read, the more it seems to me that Bakhtin foresaw many ideas which have been developed only in recent years.
Bakhtin was a Russian literary theorist and philosopher whose work offered a critique of modernist epistemologies that are based on typologies, hierarchies and dichotomies. While there are various ways of thinking about dialogue in education (see Guilherme & Morgan, 2018, for an overview), at its simplest, dialogue has three components: an utterance, a response, and a relation between the two (Holquist, 2002). We might call this relation ‘meaning’ and it appears only when a response is given. This response can be internal: the inner voice that responds to what we experience and hence gives it
personal meaning. Or the response can be an utterance that creates this relation, as well as inviting a new response and a new meaning relation. An utterance can be as basic as a single word or as elaborate as a book, song, or even a life, all of which can be construed as responses in different ways. From this starting point, we can straight away see that dialogue unfolds through time in chains of utterances and responses in a process that has no endpoint and no closure (Bakhtin, 1981). This is how we continue to make new meanings for ancient texts and reinterpret mathematics in new situations. We can also see that meaning is entirely situated: it does not reside in the utterance or the response; it is constituted by the relation between them. This situatedness is, for Bakhtin (1993), a fundamental feature of dialogism: the relations created in the moment of each utterance constitute language and the self. Meaning is not abstract or theoretical, but uniquely constituted in each unique moment.
When I worked with mathematics teachers in Pakistan (having travelled there from the UK), I came to realise that we might use the same words to talk about our teaching (e.g. ‘class discussion’), but that we meant different things. I realised this when I observed teachers ‘doing’ class discussion and it not being what I was expecting. The meaning of a term like ‘class discussion’ is situated in time and space, relating chains of utterances and responses embedded in social, cultural and linguistic histories.
In a dialogic epistemology, in which knowing emerges from dialogic relations, there is no telos, no notion of progress towards a perfect kind of knowing. To say this another way, dialogue is uncertain: we do not know where we are going. Nor is there a ‘final’ answer: meaning is always provisional, can always be revised, enriched or deepened. This is how critique and imagination are possible. Ideas that were once taken for granted have been critiqued, recast and rethought. Indeed, dialogue operates not just at the level of an individual interaction between two or more people, but between ideologies captured by common ways of talking and writing, which play into and shape specific responses at specific moments. The teachers I worked with in Pakistan brought to their utterances not just individual experience, but culturally circulating frameworks, epistemologies and ideologies about mathematics, about education, about teaching and so on, and, of course, so did I. In interacting with them, these various frameworks and assumptions became easier to discern, both for the teachers and for myself. As much as we learned about the other, we learned about ourselves.
A recurring theme in Bakhtin’s thinking is a separation between theoretical or abstract systems and the immediacy of lived experience:
Two worlds confront each other, two worlds that have absolutely no communication with each other and are mutually impervious: the world of culture and the world of life, the only world in which we create, cognize, contemplate, live our lives and die or—the world in which the acts of our activity are objectified and the world in which these acts actually proceed and are actually accomplished once and only once. An act of our activity, of our actual experiencing, is like a two-faced Janus. It looks in two opposite directions: it looks at the objective unity of a domain of culture and at the never-repeatable uniqueness of actually lived and experienced life. (Bakhtin, 1993, p. 2)
I take this to mean that our utterances (or actions) are constrained by the various socially organised systems (the world of culture), such as the ‘rules’ of language, the norms of interaction or moral principles, but are unique in their moment of utterance, reflecting our intentions, values, preferences and so on (Holquist, 2002, p. 61). We can consider mathematics in this way: mathematics is an organised system of ideas and ways of doing things, but its only reality for any of us is in the moment in which we enact it. I do not see a mathematical action as being created out of this system of ideas so much as bringing it into being in the precise moment of the utterance (within a chain of utterances ultimately going back millennia).
The dialogic nature of language and of knowing implies the dialogic nature of consciousness. This means, in particular, that consciousness depends on others. For Holquist, this is one of the keys to Bakhtin’s thought:
In dialogism, the very capacity to have consciousness is based on otherness. This otherness is not merely a dialectical alienation on its way to a sublation that will endow it with a unifying identity in higher consciousness. On the contrary: in dialogism consciousness is otherness.
We can see Fasheh’s sense of interdependence in these ideas: you exist, therefore I am. Consciousness, as knowledge of the self, is based on otherness. How does this work? Consciousness is based on the response of the other to the utterance of the self; the relation between the two gives meaning to the self. This responsive relation therefore creates tremendous responsibility; as educators, for example, we engage in prolonged responsive relations with our students and therefore contribute to the evolution of their consciousness. We should not take this role lightly. The basis of consciousness in interdependent otherness is therefore also a basis in ethics and responsibility. Indeed, for Bakhtin (1993), this ethical responsibility, for which his translators use the word ‘answerability’, is crucial for navigating a universe of relations that has no telos: “A life that has fallen away from answerability cannot have a philosophy: it is in its very principle fortuitous and incapable of being rooted” (p. 56). This answerability points again to the unique meaning of each moment: ethical responsibility is not found in theories or rules, but in the unique in-the-moment response to the other. Hence our responsibility arises at the point where we act, bringing theoretical knowing to bear in our response to whatever situation we face.
I can make sense of these ideas as a parent. My children’s consciousness is shaped more than anything by their interactions with me and their mother. As a father, I have been very aware of the responsibility this entails. For example, I want them to be conscious of their own privileged circumstances, and to care about and respect other people. At the same time, I feel a responsibility not to impose my own worldview on them, but rather to encourage them to think for themselves. In interacting with my children over the years, I have not followed a set of rules or theories but have tried to be present and aware of who my children are at in a given moment and to respond to them with care and respect.
To summarise these brief ideas about a dialogic epistemology: our knowing is interdependent with others, through systems of meaning that are multiple and in flux; meaning comes from answerability— as both response and responsibility. There is therefore scope for critique and imagination, but also uncertainty. When we address another, our interdependence implies a need for humility, not least because our words are not entirely our own—they carry the voices of many others. The application of this epistemological stance to understand the learning and teaching of mathematics I argue permits the features of mathematics education discussed in the first part of this paper. To illustrate what this might look like, I discuss what a dialogic epistemology might bring to two different situations.
Research in mathematics education has for some time grappled with questions arising from the increasing diversity found in mathematics classrooms in terms of languages and cultural backgrounds. Such questions are usually framed from a dominant linguistic and/or cultural perspective usually occupied by the mathematics teacher. For example, in my own research, I have examined language diversity in mathematics classrooms in England, where English is the only language of instruction. Children who speak other languages might be labelled as learners of English as an additional language, or emergent bilinguals, with English as the reference point. Moreover, such children create ‘challenges’ or ‘problems’ for teachers or else their status as learners of English involves ‘obstacles’ or ‘problems’ for the children. I have conducted work in contexts of language diversity in Canada, where English or French are the dominant languages, with similar positioning involved. The dominance of some languages reflects the social stratification of language, driven by what Bakhtin (1981) calls centripetal forces. These forces are in tension with centrifugal forces which reflect the creative diversity of human interaction. Standardisation of languages or particular forms of language result in various ‘theoretical’ languages, but each utterance reflects a unique living moment. Learning mathematics, for the learner, means learning a language (a repertoire of responses) of mathematical others, what Bakhtin called an alien word. The inscription of the language of mathematics in curricula, textbooks and institutions make it a powerful language, driven by the centripetal forces of standardisation of a mathematics register, its
symbol system and so on. Learners must therefore appropriate this language and, in some sense, submit to it.
As part of my doctoral research in England, I asked learners of English as an additional language aged 10-11 years old to work in pairs to write arithmetic word problems. Looking back at this work now, I can see the task as an opportunity for the children to respond to the word problems they had so often encountered in their mathematics classrooms in England or, in some cases, elsewhere in the world. Word problems are notorious for being highly culturally situated, as well as linguistically peculiar, although they have existed for millennia. Here are a couple of examples of what the children came up with:
There are a hundred and eighty brains in the morgue. Four monsters came and eat 44 each. How much is left?
I have 150 cars in my business. Group these into 3 groups to see if you’re clever.
The children who wrote these word problems create meaning through the relation between the problems they create and the standard genre of arithmetic word problems. In the case of the first problem, the sense of mathematics as an alien word can be surmised from the atypical situation on which the problem is based. These students have applied the word problem genre to a novel situation derived from their own experiences and interests. As such, their own values are expressed in the moment of the creation of their word problem. The second problem concisely offers a critique of the entire purpose of solving word problems, setting in relation the banal requirements of standard form with a child’s-eye sense of what they are really for. In both cases, the (multiple) meaning of each problem arises from its relation with the word problem genre and the many such problems these children have encountered during their schooling. In other work, I have examined the social nature of word problems (Barwell, 2018a) and how for children, in addition to mathematics, they bring up issues of identity, lived experience and language (Barwell, 2003, 2005a, 2005b).
In research in Canada, I participated in an exchange with two students of Indigenous Cree backgrounds in which a mathematical word problem was alienating in several ways. These children came from small communities in the north of Quebec and grew up speaking the Cree language. The problem, which was of a type used in provincial assessments, began with a 90-word paragraph about a tulip festival that takes place in Ottawa every spring. The problem invited students to imagine they are gardeners and asked them to complete a tulip display in a pattern of increasing squares, as shown in a diagram (Figure 2). The introductory paragraph had little direct relevance to the mathematical task.
I had been asked to work with the two students on the problem. We read the problem through and then I asked them what it was about.
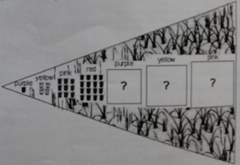
Figure 2: Part of the tulip problem
Curtis: it’s about (.) world’s biggest flower=I don’t know RB: ottawa’s biggest
Curtis: tu (.) lip festival
RB: tulip festival (.) do you know any of those? (.) do you know what a tulip is? [hm Curtis: [flower
RB: flower right (.) have you ever seen a tulip? […]
Ben: (…) it’s white
RB: they are lots of different colours white ones red ones Curtis: like a rose?
RB: yellow ones say again
Curtis: rose
RB: no it’s a bit different from a rose (.) roses yeah (.) tulips just come up in the spring and have a nice flower for about two weeks (.) then they are finished (.) there we go (.) let me see your picture
Ben, Curtis: [laughter]
RB: have you seen flowers like that Ben: ^no^
Curtis: yeah (.) in a store
It seems clear that the scenario described in the problem was not familiar to the two students. Tulips do not grow in the communities where they grew up and still spent much of their time. They had likely not visited the tulip festival. Once we got past the scenario and focused on the pattern, they were able to find a solution quite quickly. It took considerable further work, however, to produce a written explanation of their solution (see Barwell, 2014, 2016).
The problem arguably alienated the students in a few different ways (see Barwell, 2016, for a detailed analysis). The text was in English, which was not the main language the students spoke in their communities. English represents the history of colonisation of Canada, instantiated through laws that make English and French the official languages of education. The references to the tulip festival indexed a particular kind of Canadian-ness that is familiar with events in the national capital. The problem assumed children have become familiar with the complicated textual genres found in mathematics classrooms. And, of course, there was the mathematical component of the problem and the valuing of written reasoning and explanation over situated oral explanations. The problem was therefore tied into a web of social stratification that relates languages, cultural knowledge, national identity and mathematical performance. Unfortunately, this stratification positioned the students outside the expected norms. And yet to succeed in school mathematics, students must learn to work in relation to these norms.
What, then, is the responsibility of mathematics teachers towards children from marginalised backgrounds? The awareness that mathematics teachers participate in the realisation of students’ consciousness (sometimes referred to as ideological becoming) brings an ethical responsibility. What kind of mathematical consciousness do we want students to have? Do students have “freedom to learn and to act”? Can they be themselves? Or must they adopt and enact pre-determined ways of talking and doing mathematics? A dialogic perspective enables us to understand the students’ responses not as ignorance of culturally assumed information, or perhaps as facing cultural and linguistic barriers to success, but rather as reflecting the relationality between the knowledge that they bring and the knowledge embedded in the problem.
These questions bring to mind Bakhtin’s contrast of authoritative discourse and internally persuasive discourse. The former aligns with a monologic ideal which, in mathematics classrooms, might be reduced to the idea that there is a right way and a wrong way to do mathematics. From this perspective, we might conclude that Curtis and Ben should know what a tulip is; if they do not, they should be taught it, so that they can succeed in the standard institutionalised mathematics. Students are, in this view, expected to learn the right ways.
The authoritative word demands that we acknowledge it, that we make it our own; it binds us, quite independent of any power it might have to persuade us internally; we encounter it with its authority already fused to it. The authoritative word is located in a distanced zone, organically connected with a past that is felt to be hierarchically higher. It is, so to speak, the word of the fathers. Its authority was already acknowledged in the past. It is a prior discourse. It is therefore not a question of choosing it from among other possible discourses that are its equal. It is given (it sounds) in lofty spheres, not those of familiar contact. (Bakhtin, 1981, p. 342).
How many students experience mathematics in this way? Many? Most? Not all, certainly; some are able to develop an internally persuasive mathematical discourse. For Matusov and von Duyke (2010), internally persuasive discourse means:
a dialogic regime of the participants’ testing ideas and searching for the boundaries of personally-vested truths. In this approach, “internal” in [internally persuasive discourse] is interpreted as internal to the dialogue itself in which everything is “dialogically tested and forever testable” (Morson, 2004, p. 319). (p. xx)
This is a strong claim. Internally persuasive discourse is not simply convincing oneself of something, but rather a dialogic process within which an utterance, subject to being tested, is persuasive, at least provisionally. In contrast, authoritative discourse is, in its purest form, not dialogic at all (and is, therefore, in view of the earlier definition of dialogue, meaningless, as many students can unfortunately attest). What would internally persuasive discourse involving Curtis and Ben look like? Perhaps the word problems I cited from the earlier research gives some hints.
At this point, you are probably agreeing that internally persuasive discourse in mathematics classrooms is what we want, since we want mathematics to be meaningful, relevant and connected to our students’ lives. How can we create classrooms around this idea? We might turn to pedagogical ideas like landscapes of investigation (Skovsmose, 2001), in which students are invited to explore different situations using mathematics and other ways of knowing. Or we might turn to decolonial interactions, as illustrated by Parra in his plenary address at the Mathematics Education and Society conference in 2021. There are, however, some tensions to navigate.
In a paper entitled ‘What if I was harmful?’, Abtahi (2022) explores some of these tensions in the context of her teaching of a course on mathematics pedagogy within an Indigenous Teacher Education Program in Canada. Aware of the distinctive cultural and linguistic heritage of her students, Abtahi adopted a strategy that many of us might endorse: she created spaces for her students to bring cultural resources of their own into the mathematics around which the course was designed (based on the curriculum of the province of Ontario). Reflecting on her experience, however, Abtahi considers whether her approach may have been ignorant or even harmful:
I could have been ignorant because I did not pay attention to the fact that the cultural resources that I selected may not have greater value to members of the community in question than many of the other resources within that community. This kind of inclusion of cultural and other resources takes no account of the community’s distinctive value systems, which might have nothing to do with mathematics (at least as represented in a curriculum). Therefore, such an approach, regardless of how well intentioned it might be, risks trivialising the cultural resources of the community. It invests these resources with mathematical meanings from the “outside”—meanings that may not have any connection with those invested in them by members of that community. I could have been harmful, because I did not pay attention to whether and in what ways the type of (mathematical) knowledge that I had brought with me, as presented in the culturally misaligned Ontario mathematics curriculum, affected the cultural, linguistic and social resources of my students and, in particular, the resources and the wholeness of the integrated practices that make them the selves that they are-in-relations. (p. 163)
Abtahi draws out an important set of tensions that are connected with the relation between self and other, in this case, between teacher and learner. If our teaching of mathematics contributes to the consciousness of our learners, and if we conduct our anti-oppressive teaching in a way that is still inscribed within broader social structures and relationships of dominance and oppression, then our teaching may nevertheless be harmful.
How else can we imagine interactions in a mathematics classroom like the one discussed above, with language diversity and cultural diversity? A dialogic epistemology brings a focus on the unique moments of each utterance and the relationality that links the students, their teacher, the words in a word problem and wider institutional and societal norms, on the responsibilities of each towards the other, and especially of those who are aligned with the expected centripetal norms towards those who may be marginalised by these same norms.
At the start of this paper, I drew attention to the dire state of our planetary ecosystem. Mathematics educators are increasingly thinking about how the learning and teaching of mathematics should respond to this crisis (e.g., Barwell, 2018b, 2022; Barwell, Boylan & Coles, 2022; Coles et al., 2013; Gútierrez, 2017). Mathematics is implicated in this crisis: mathematics is used to describe the crisis, to predict what will happen in future, and to communicate about it (Barwell, 2018b). Mathematics is also integral to the extractive consumption-based economic system that is contributing to the crisis, not least through its role in digital technologies, as Skovsmose (2021), among others, has pointed out. There is also a more fundamental way that mathematics is implicated. Mathematics is embedded in discourses of control, domination and mastery of people, other species, and ecosystems. These are the same discourses that are implicated in racism, neocolonialism, classism, and other oppressive structures. Let me give an example about wolves. I will summarise some different ways of thinking about wolves.
Ecology: Wolves are an important part of many northern-hemisphere ecosystems, ranging across North America and Eurasia. Ecologists have analysed how the presence of wolves impacts the whole web of relationships that make up an ecosystem (Eisenburg, 2010). Wolves predate deer, for example, which regulates deer population, preventing over-grazing and allowing forest regeneration. The presence of wolves also affects the behaviour of deer who are more cautious and graze less heavily in exposed places. One impact is heavier growth of trees and shrubs along water courses, which ensures better conditions for fish species that need shade and slow-flowing water. And so on…an intricate web of interconnected life.
Culture: Wolves are significant in many cultures. In European traditional stories, wolves are to be feared. The wolf eats Little Red Riding Hood’s grandma and attacks the Three Little Pigs, destroying their houses. In versions of both stories, the wolf is eventually destroyed. These stories continue to be told in the UK, despite the elimination of wolves in the British Isles by the seventeenth century. In many North American traditions, wolves are our relatives and not to be feared. In one story, told by John Johnson Sr., President of the Lac du Flambeau Band of Lake Superior Ojibwe:
2
Wolf and first man were brothers. They were companions. Creator told them to walk together on the earth and to name all the plants and animals. When they finished naming all of the animals and all of the plants, the Creator told Ma’iingan and First Man they could no longer live together; it was time for them to go down separate paths, but from then on, they must look out for each other.64F
Politics: The Eurocentric fear of wolves is apparent in continuing attempts to reduce their presence or eliminate them entirely in different parts of the world. In recent years, culls or significant levels of hunting have been reported in, for example, British Columbia, Minnesota, Montana, Wisconsin,
https://nativeland.info/blog/uncategorized/wolf-and-first-man-an-anishinaabe-story-of-companionship-and-protection-amid-the- growing-threats-of-poachers-and-habitat-loss/
Norway, Sweden and Finland. Justifications for culls are typically about protecting livestock or species of other economic value, such as caribou, who are themselves hunted by humans. Reporting highlights tensions between farmers, conservationists and Indigenous peoples. Much of the reporting uses language like managing wolf populations, harvesting wolves efficiently, and protecting farmers and their livelihoods. In a report of a hunting season in Wisconsin, for example, we read:
In just three days this week, Wisconsin hunters killed nearly twice the number of wolves that wildlife managers had intended to be harvested in a brief, court-ordered hunting and trapping season. Hunters killed 216 wolves between Monday and Wednesday, well past the 119 quota set by the Wisconsin Department of Natural Resources […] Before the hunt, the population was estimated to be around 1,200 wolves. The quota was set with the goal of keeping the population stable, [the director of the state wildlife management program] said.
Note that the hunt resulted in a reduction of the wolf population in the state of almost 20 per cent in three days, as a measure to ensure “stability”.
Mathematics: Estimating wolf-populations and understanding how they change over time, including as a result of culls, hunts and illegal poaching, involves mathematical modelling and statistical methods. For example, Marescot et al. (2012) start with something called probabilistic stage-structured matrix models based on the social organisation of wolf populations. Wolf packs include juveniles, dispersers (who leave the pack), subordinates and alphas. Marescot et al. show how a four-stage model based on reproduction, dispersal and mortality can be simplified to a single-stage model based on female Alpha wolves. Since there is only one alpha female in each pack, it is enough to count or estimate the number of packs, rather than the number of individuals, which is much more difficult. The model includes multiple parameters: fertility rate, survival rates of different categories of wolf, probability of dispersing and of establishing a new pack, and asymptotic growth rate.
In what I have briefly summarised above, mathematics appears as a tool for managing wolves. Mathematical modelling turns wolves into parameters, while wildlife management authorities may use such models to establish hunt quotas. While ostensibly ‘scientific’, this way of working is based on an extractive, human-centric perspective that sees humans as masters of the ecosystem, human needs and desires as the most important, and wolves as creatures to fear and destroy. It represents mathematics as the authoritative word. There is little dialogue with a gun. What consciousness does this suggest for wolves? The story of wolf and first man suggests a different kind of relationship. In the text of her address to the Mathematics Education and Society conference in 2019, Gutiérrez writes of a mathematics of dispossession. The mathematical models and methods of estimating wolf populations contributing to dispossessing wolves of their territory, their freedom and their lives, as well as dispossessing the ecosystem of one of its species. What if our consciousness depends, in part, on wolves? Are we dispossessing ourselves? I think we are.
How can we think about a mathematics education that is answerable—responsible—to wolves? That recognises their intrinsic worth, their right to exist? Gutiérrez draws on North American Indigenous perspectives to propose three notions that can contribute to answering this question: interdependence (‘In Lak'ech’ in Mayan), indeterminacy (‘Nepantla’ in Nahuatl) and reciprocity. She advocates for “recognising self and/in others, responsibility towards others, and valuing tensions” (p. 15). This perspective has striking similarities with the dialogic epistemology I have summarised, as well as the contributions discussed in the first part of this paper. From this perspective, we must think about doing and learning mathematics in relation to wolves in such a way that we see ourselves in them.
Each time we act in mathematics in relation to the living world, we are offering a response—creating meaning. Hence, we are responsible; there is an ethical dimension to our mathematical action. As well as helping us to see this, a dialogic epistemology suggests some ways to think about mathematics and mathematics classrooms. Each time we act in mathematics, we bring mathematical into being and we have some agency with respect to what it is like. Different mathematical worlds are possible, and some of them may not look like the mathematics we are familiar or comfortable with. Some mathematical worlds may not look like mathematics at all. What kind of mathematical world does a wolf bring forth?
What kind of mathematics does the living planetary ecosystem bring forth? Standard mathematical curricula do not give much space to these kinds of questions. Responding to them requires imagination. One approach is to set mathematics in relation to other ways of knowing, such as art, story, myths or poetry, through reading/viewing such work or by creating it.
The world is in trouble and mathematics is implicated. What is our responsibility? I have attempted, probably not entirely successfully, to work with the idea that we are all related: humans, animals, plants, fungi, rocks, rivers and oceans. Our knowing of mathematics is interdependent with our knowing of each other; there is no absolute knowing or knowledge outside of these relations. As a result, we have some responsibility to others in all the mathematics that we do. In our work as teachers, teacher educators and researchers, I think this means fulfilling these roles with an awareness of the ethical relations between us and with a sense of humility that comes from the awareness that we depend on each other to know what we know and that there is much that we do not know. We depend on the wolf to show us what she knows of the forest, as the wolf depends on us to learn to treat the forest with respect. We depend on children to show us what they know of mathematics (or anything else) as our children depend on us in their developing consciousness. We depend on each other to become aware of the ideologies, epistemological frames and oppressive assumptions that we all inherit. It is only through dialogue with others that we can ever move towards this awareness. This is why we need to ensure the survival with dignity of languages, cultures and species. A sense of humility comes too from the awareness that there is much that we do not know and that we do not have any privileged place in our ecosystem. Such uncertainty suggests we, as a species, need to listen to many voices in the choices that we make. Opening new lands for oil drilling or deforestation do not seem to me like choices filled with humility or uncertainty, however many graphs and models may be used to support them. Our responsibility means that we must proceed with imagination and critical awareness, willing to critique ourselves as much as others, to try new ideas knowing that they may fail, but knowing that sometimes that this is better than repeating old ideas and failing. As teachers, we are responsible for the future of our children. As mathematicians we are responsible for the ethical use of different versions of our subject for the future of our society and our planet. As researchers we are responsible to imagine and to critique. For me, this is a hopeful perspective. There is hope in our interdependence, hope in imagination, hope in critique because it creates the possibility for change.
Abtahi, Y. (2022). What if I was harmful? Reflecting on the ethical tensions associated with teaching the dominant mathematics. Educational Studies in Mathematics, 110(1), 149–165.
Bakhtin, M. M. (1981). The dialogic imagination: Four essays. University of Texas Press. Bakhtin, M. M. (1993). Toward a philosophy of the act. University of Texas Press.
Barwell, R. (2003). Patterns of attention in the interaction of a primary school mathematics student with English as an additional language. Educational Studies in Mathematics, 53(1), 35–59.
Barwell, R. (2005a). Empowerment, EAL and the National Numeracy Strategy. International Journal of Bilingual Education and Bilingualism, 8(4), 313–327.
Barwell, R. (2005b). Working on arithmetic word problems when English is an additional language.
British Educational Research Journal, 31(3), 329–348.
Barwell, R. (2014). Centripetal and centrifugal language forces in one elementary school second language mathematics classroom. ZDM, 46(6), 911–922.
Barwell, R. (2016). Investigating stratification, language diversity and mathematics classroom interaction. PNA, 11(1), 34–52.
Barwell, R. (2018a). Word problems as social texts. In K. Yasakuwa, A. Rogers, K. Jackson & B. V. Street (Eds.), Numeracy as social practice: Global and local perspectives (pp. 101–120). Routledge.
Barwell, R. (2018b). Some thoughts on a mathematics education for environmental sustainability. In P. Ernest, P. (Ed.), The philosophy of mathematics education today (pp. 145–160). Springer.
Barwell, R. (2022). In dialogue with Planet Earth: Nature, mathematics, and education. In C. Michelsen,
A. Beckmann, V. Freiman, U. T. Jankvist & A. Savard (Eds.), Mathematics and its connections to the arts and sciences: 15 Years of interdisciplinary mathematics education (pp. 109–120). Springer.
Barwell, R., Boylan, M. & Coles, A. (2022) Mathematics education and the living world: A dialogic response to a global crisis. Journal of Mathematical Behavior, 68, 101013.
Coles, A., Barwell, R., Cotton, T., Winter J. & Brown, L. (2013) Teaching secondary mathematics as if the planet matters. Routledge.
D’Ambrosio, U. (2010). Mathematics education and survival with dignity. In H. Alrø, O. Ravn & P. Valero (Eds.), Critical mathematics education: Past, present, and future (pp. 51–63). Sense.
D’Ambrosio, U. (2015). From mathematics education and society to mathematics education and a sustainable civilization: A threat, an appeal, and a proposal. In S. Mukhopadhyay & B. Greer (Eds.), Proceedings of the eighth international mathematics education and society conference (vol. 1, pp. 19– 30). Ooligan Press.
Eisenberg, C. (2013). The wolf's tooth: Keystone predators, trophic cascades, and biodiversity. Island Press.
Fasheh, M. (2015). Over 68 years with mathematics: My story of healing from modern superstitions and reclaiming my sense of being and well-being. In S. Mukhopadhyay & B. Greer (Eds.), Proceedings of the eighth international mathematics education and society conference (vol. 1, pp. 33–60). Oolingan Press.
Guilherme, A. & Morgan, W. J. (2018). Philosophy, dialogue, and education: Nine modern European philosophers. Routledge.
Gutiérrez, R. (2017). Living mathematx: towards a vision for the future. In E. Galindo & J. Newton (Eds.), Proceedings of the 39th annual meeting of the North American chapter of the International Group for the Psychology of Mathematics Education (pp. 2–26). Hoosier Association of Mathematics Teacher Educators.
Harraway, D. J. (2016). Staying with the trouble: Making kin in the chthulucene. Duke University Press. Holquist, M. (2002). Dialogism (2nd ed.). Routledge.
Hulme, M. (2009). Why we disagree about climate change: Understanding controversy, inaction and opportunity. Cambridge University Press.
Intergovernmental Science-Policy Platform on Biodiversity and Ecosystem Services (IPBES) (2018).
Assessment report on land degradation and restoration. IPBES.
Intergovernmental Science-Policy Platform on Biodiversity and Ecosystem Services (IPBES) (2019). Media release: Nature’s dangerous decline ‘unprecedented’, Species extinction rates ‘accelerating’. Available from: https://ipbes.net/news/Media-Release-Global-Assessment
Jenkins, C. N., Pimm, S. L. & Joppa, L. N. (2013). Global patterns of terrestrial vertebrate diversity and conservation. PNAS, 110(28), E2602–E2610.
Lovelock, J. (2009). The vanishing face of Gaia: A final warning. Basic Books.
Marescot, L., Gimenez, O., Duchamp, C., Marboutin, E., & Chapron, G. (2012). Reducing matrix population models with application to social animal species. Ecological Modelling, 232, 91–96.
Matusov, E. & von Duyke, K. (2010) Bakhtin’s Notion of the Internally Persuasive Discourse in Education: Internal to what? (A case of discussion of issues of foul language in teacher education). In
K. Junefelt & P. Nordin (Eds.), Proceedings from the second international interdisciplinary conference on perspectives and limits of dialogism in Mikhail Bakhtin (pp. 174–199). Stockholm University.
Morton, T. (2010). The ecological thought. Harvard University Press.
Parra, A. (2021). Mathematics education, researchers and local communities: A critical encounter in times of pandemic, pareidolia and post-factualism. In D. Kollosche (Ed.) Proceedings of the eleventh international mathematics education and society conference (vol. 1, pp. 65–80). Tredition.
Skovsmose, O. (2001). Landscapes of investigation. ZDM, 33, 123–132.
Skovsmose, O. (2015). Uncertainty, pedagogical imagination, explorative reasoning, social justice, and critique. In S. Mukhopadhyay & B. Greer (Eds.), Proceedings of the eighth international mathematics education and society conference (vol. 1, pp. 111–124). Ooligan Press.
Skovsmose, O. (2021). Mathematics and crises. Educational Studies in Mathematics, 108(1), 369–383.