https://doi.org/10.34024/prometeica.2024.31.15962
EXPLORANDO IDENTIDADES MATEMÁTICAS DE JOVENS BEM-SUCEDIDAS EM MATEMÁTICA PÓS-OBRIGATÓRIA
EXPLORANDO LAS IDENTIDADES MATEMÁTICAS DE MUJERES JÓVENES EXITOSAS EN MATEMÁTICAS POSTOBLIGATORIAS
Emilie Gertz
(Universidade de Copenhague, Dinamarca)
Recibido: 30/11/2023
Aprobado: 29/11/2023
RESUMO
Este artigo tem como objetivo explorar as identidades matemáticas de 33 jovens mulheres à medida que se deparam com a matemática pós-obrigatória do ensino secundário. Todos optaram por progredir em matemática até o nível A, o que os separa de muitos outros jovens estudantes em todo o mundo. Através de um quadro de identidade composto por quatro componentes inter-relacionados (competência, desempenho, interesse e reconhecimento), foram realizadas e analisadas entrevistas narrativas com elas para explorar a interação entre as jovens e o contexto educacional disciplinar. Os resultados mostram uma idealização de um caminho estreito para a identificação com a matemática para aqueles selecionados que conseguem produzir respostas corretas. No entanto, a variação no caminho para o sucesso está relacionada com a forma como eles se veem como trabalhadores esforçados ou como possuidores de competências matemáticas especiais. A identificação destas diferenças oferece uma compreensão mais ampla da identificação das jovens com o sucesso em matemática.
Palavras-chave: identidade matemática. pós-obrigatório. gênero.
ABSTRACT
This paper aims to explore the math-identities among 33 young women in their meeting with post-compulsory upper secondary school mathematics. They have all chosen to advance mathematics to A-level, separating them from many other female students around the world. Through an identity framework consisting of four interrelated and overlapping dimensions (competence, performance, interest, and recognition) narrative interviews were conducted and analyzed to explore the interplay between the young women and the disciplinary educational context. Findings show an idealization of a narrow route to identify with mathematics for the selected ones who can produce correct answers. However, variation in the route to success relates to how they see themselves as either hard working or possessing special abilities for mathematics. The identification of these differences offers a broader understanding of successful young women’s identification with mathematics.
Keywords: mat-identity. post-compulsory. gender.
RESUMEM
Este artículo tiene como objetivo explorar las identidades matemáticas de 33 mujeres jóvenes en su encuentro con las matemáticas de la escuela secundaria superior post- obligatoria. Todas han optado por avanzar en matemáticas hasta el nivel A, separándolas de muchas otras estudiantes jóvenes de todo el mundo. A través de un marco de identidad que consta de cuatro componentes interrelacionados (competencia, desempeño, interés y reconocimiento) se realizaron y analizaron entrevistas narrativas con ellas para explorar la interacción entre las mujeres jóvenes y el contexto educativo disciplinar. Los hallazgos muestran una idealización de una vía estrecha para identificarse con las matemáticas para los seleccionados que pueden producir respuestas correctas. Sin embargo, la variación en la ruta hacia el éxito se relaciona con la forma como se ven a sí mismas como arduas trabajadoras o como poseedoras de habilidades especiales para las matemáticas. La identificación de estas diferencias ofrece una comprensión más amplia de la identificación de mujeres jóvenes exitosas con las matemáticas.
Palabras clave: identidad matemática. post-obligatoria. género.
Introduction
Around the world mathematics is considered an important school subject. It plays an important role in compulsory schooling and functions as a gatekeeper for a variety of educations and career opportunities (Anderson et al., 2015; Mendick, 2005). At the same time mathematics is often perceived as a special subject and considered difficult and hard (Boaler & Greeno, 2000) and many students struggles with mathematics at compulsory level (Anderson et al., 2015; Jaremus, 2021; UVM 2022). Especially in western countries, girls choose not to continue into post-compulsory mathematics (Jaremus, 2021) and in general students identifying as ‘good at mathematics’ in post- compulsory schooling are rare (Mendick, 2005).
An equitable approach to mathematics (UNESCO, 2017) would therefore call for a broader understanding of students’ possibilities for engaging and participating. A starting point is to understand the ideals that effect our perception of who does mathematics. One step in this direction is to understand the female students who choose post-compulsory mathematics and how they are able to see themselves and be seen by others in the discipline. This will add to the research on gender and mathematics as research has mainly focused on either girls and young women who disengage from mathematics, or women in higher education and their challenges with navigating a positive relationship with mathematics (Radovic et al., 2017). Furthermore, this will challenge the traditional approach to research on gender and mathematics, as this has often focused on differences between boys/men and girls/women, and thereby treated girls and women as a homogenous group (Jaremus, 2021).
In this regard Denmark becomes an interesting case. First, because among the students who continue into post-compulsory mathematics in upper secondary school the majority are women (61%; GL, 2020). Second, because the proportion of female students who choose to advance with mathematics to the highest level (A) is greater than that of male students (57%). Last because the young women in general perform on par or better than the young men in mathematics (DE 2019). In addition, Denmark is at the top at the Social Progress Index which rank the countries on their ability to provide basic social needs for their citizens. This means that Danish young women are living in a highly developed country, that many of them continue into post-compulsory mathematics, choose to advance the subject and are good at it. This raises an interesting question: In what way do they see themselves and are they seen in mathematics? I therefore aim to explore young women’s experiences and expectations when doing mathematics, how they see themselves and are seen by others as performing female math-students. This approach will contribute with knowledge on cultural and social aspects of learning mathematics. From here we can gain insights into ways young women do post-compulsory mathematics and reach an
understanding of the different negotiations and meaning making young women perform within the discipline.
Theoretical framework
For decades research in mathematics education has turned the focus towards identity (Darragh, 2016) emerging different approaches to understand students’ learning and engagement with mathematics (Radovic et al., 2018). In this paper I draw on a theory of identity, developed in science education by Carlone & Johnson (2007) to study science identities and validated for math-identities by Cass et al. (2011). This framework is modeled largely off Gee’s (1999, 2000) work where identity is understood as being recognized as a ‘kind of person’. It offers a way to explore the interplay between a student and a specific disciplinary educational context, in this case upper secondary school mathematics. The framework holds four interrelated and overlapping dimensions to explore a student’s math-identity (Cass et al., 2011):
Competence : Knowledge and understanding of mathematics. Performance : Social performances of relevant mathematical practices. Interest : Desire/curiosity to think and understand in mathematics.
Recognition : Recognizing oneself and being recognized by others as being a “math-person”.
Identity is not just about seeing oneself as someone but also about being recognized as someone. It emerges out of the possibilities and limitations available in a local setting, accessible as a result of an individual’s interest, competence, and performance, while being recognized by meaningful others (Carlone & Johnson, 2007). Identity is not to be understood as something stable or inherent. Following Butler (1990) identity as well as gender is constantly performed and negotiated and thus not something that one is born with or possesses. With this theoretical framework I can explore how the young women experience what is promoted and marginalized in their meeting with upper secondary school mathematics, as well as how they negotiate and make meaning of these experiences.
Methodology
I draw on data from my ongoing Ph.D. project on young women in the Danish upper secondary school. The project is a qualitative longitudinal study and focuses on young women’s choice of science and mathematics, their development of science and math-identities during the education, as well as their aspirations for the future. The first round of data consists of a survey and 33 individual interviews with young women. In this paper I will focus on the data concerning the young women’s experiences with and expectations to mathematics during the first year in upper secondary school.
In Denmark the primary and lover secondary education (Grundskole) consist of compulsory grade 0 to 9 (age 6 till 16). After 9th grade one can choose to enter either upper secondary education or vocational educating and training. The upper secondary educational programs consist of four academically oriented schools where the 3-year upper secondary school (STX) is the most chosen one (60%; GL, 2021) with a predominance of young women (61%; GL, 2020). This education prepares the students for further studies and provides access to higher educations. The upper secondary school has a range of compulsory subjects all divided into levels (A, B and C - A is highest and C lowest) and different specialized study programs containing 2-3 subjects at specified levels (DES, 2016). Each student must choose a specialized study program which is chosen in the beginning of the first year. All educations are free of
admission and non-refundable state grants to cover living expenses are given to students older than 18 years.
The participants in the study all identified themselves as being young women. They all chose mathematics at the highest level (A) and are enrolled in three different study programs combining mathematics with social science, with biotechnology and physics, and the last with physics and chemistry. The young women are located on three different upper secondary schools differing in the socio-economic references, the size of the school, the distribution of female students and the schools overall grade point average. They were selected through a survey distributed to a total of 148 students, where 75 identified themselves as young women. The survey had mostly open-ended questions and asked into background, lower secondary school experiences, upper secondary school experiences, future considerations and whether they would volunteer for individual interviews with me. Forty-seven young women volunteered and in total 33 were selected to participate in the interviews. Different aspects were considered in the selection process to obtain a maximum variation of prior and current relationship with mathematics and science combined with background and ethnicity (Flyvbjerg, 2011). Thirteen out of the 33 came from an academic background and a small group out of the 33 had a minority ethnic background. Hence, the sample provided access to a wide range of circumstances the young women were situated in.
The interviews with the selected young women were conducted individually at the schools, during schooltime, and lasted between 40 to 60 minutes. I had previously been visiting each class so that the young women knew about me and the study. Just before the beginning of each interview, I informed about anonymity, confidentiality, and data protection and the interviewee signed a consent form following the ethical guidelines at University of Copenhagen.
The interviews were conducted as semi-structured (Kvale and Brinkmann, 2009) and with a narrative interview approach (Andrews et al., 2008) where focus is on encouraging the interviewees to share and elaborate their narratives. Four main themes drove the interviews: 1. Upper secondary school experience in general, 2. Experiences with mathematics, 3. Experiences with science, 4. Future perspectives. As well as four specific themes: I. Prior experience with mathematics and science, II. Expectations to mathematics and science, III. Transition into upper secondary school, IV. Considerations when choosing the study program. All themes were covered in the interviews but the distinction between main and specific indicated a difference in range of the questions. The main themes were open meaning the interviewees could take the conversation in different directions. Whereas with the specific themes the focus was narrower and therefore the questions were more closed. All interviews were audio-recorded and transcribed. Here information traceable to the participants was anonymized. To conceal the identities of the young women I have used pseudonyms and left out specific information that would potentially identify them.
A thematic approach (Braun & Clarke, 2006) was used to analyse the transcriptions. This was coded in Nvivo and driven by two analytical questions:
Q1: How do the young women narrate their construction of math-identities in upper secondary school mathematics?
Q2: How do the young women make meaning of their experiences in upper secondary school mathematics?
The transcriptions were first read individually to gain an understanding of each young woman. Then read across the 33 young women to identify patterns and topics in the narratives and create themes. Last, the themes were contextualized by re-reading the individual transcriptions. To answer the first analytical question (Q1) the themes were established both inductively and deductively driven by the theoretical framework (the four dimensions: Competence, Performance, Recognition, and Interest). The second question (Q2) was answered inductively only. The analysis was reflexive constantly moving back and forth between the different steps.
Findings
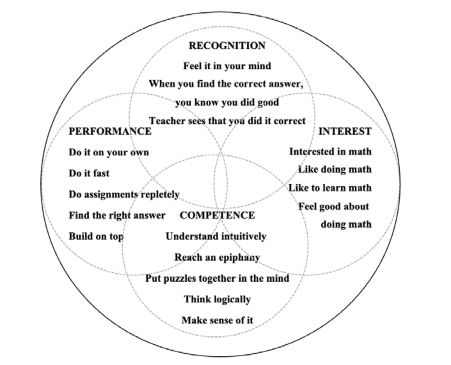
The findings are structured around the identity dimensions expressed in the narratives, shared by the young women in the interviews. Their construction of a math-identity and the role of the different dimensions within, is presented in the first part of the findings. The last part presents how the young women make meaning of their experiences in upper secondary school mathematics. In figure 1 an outline is presented of the identity dimensions in the young women’s narratives:

The outermost circle represents the context, here upper secondary school mathematics, and the four overlapping circles refer to the four dimensions in the identity framework and represent the possibilities and restrictions for constructing an identity within the context. The four circles highlight keywords in the young women’s experience of: Competences, performances, and interests in mathematics, as well as what was recognized as doing mathematics by oneself and by others. In the following the young women’s construction of the dimensions are unfolded. The themes are presented as four separate themes, as to provide analytical clarity. However, they are informed by the interrelated and overlapping dimensions in the identity framework and therefore not seen as something separated in the construction of identity.
In the young women’s narratives math-competences were described as rational and logical thinking and something embedded in the mind. As an example, several of the young women explained how the
competences entailed an intuitively understanding of logical structures. One of the young women Sara explained “I think that I’m good at understanding…that if this…then that, and then you can use this to…move further”. This understanding was described as something that appeared in the mind as an epiphany, as something that just made sense, something that stuck to the mind, or a code that was cracked. A young woman Ella described such competence as a finger-snap and said “...I got it…it is something new I learned. That’s really nice”. Others described it like a game solitaire in the mind won by thinking logically, or as a mind-puzzle where all the pieces fitted together. As a consequence, other ways to learn and understand like being playful or creative were regarded less important. Amalie talked about how playfulness had disappeared in upper secondary school mathematics. In lower secondary they had done activities with shooting basketball hoops and creating functions out of the ball’s direction. When asked about if she missed these other ways of doing mathematics, she replied “I’m not sure if I got anything out of it…it was more just for fun”. So, playing with mathematics or doing experiments was not recognized as learning. Also, Alma explained that she found social science and Danish more difficult to do, because then she had to get her creative brain going, whereas mathematics was “just black/white”. Thus, creativity was not something that she experienced needing, as mathematics consisted of indisputable answers.
One of the shared narratives about how to properly perform mathematics was the act of reaching epiphanies through working with assignments. A young woman Helena explained that when learning a new topic, the class would always do assignments and here she would suddenly get an epiphany and go “oh that’s the way to do it”. Another young woman Ellen said “if [the teacher] feels that we haven’t understood it, then we do some more assignments”. So, doing assignments was recognized as a way to gain understanding. Such performance was also narrated as something that was done repeatedly in every lecture, and some narrated it as a practice done fast and alone. A young woman Mia explained that “some like to sit and talk about the assignments. I would rather do them individually, so I just zone-out”. Others also narrated the performance as something that they liked to do on their own. Rose talked about doing assignments as being really relaxing and nice to do by herself.
Doing assignments was highlighted as something positive and as a comfortable, concrete, and predictable way to perform in mathematics. Comfortable and concrete because one would know what to do – just follow the rules and use the formulas like Alma and Helena:
Alma: It is pretty clear what I need to do, like, I have formulas, and I need to do like this and it works like that. That’s really nice.
Helena: …you just sit and do the assignments, like you use and reuse these formulas and proofs...
Predictable because the procedure would always end up with one correct answer: Helena: [I like] that there is only one answer.
Selda: I love when there is only one correct answer… Vilma: [I like] that there is an answer…one correct answer.
Sara: There is this simple answer that it should end up with. That I really like.
Predictability was not only in the process of finding the correct answer, but also in the resolution to not being able to find it. One of the young women Selda explained that when she did not get the correct answer, she knew that she had done something wrong and that she could “go back and look through the different steps”. This element of revision of own process when not finding the correct answer was likewise highlighted by others. Astrid explained that “if it does not make sense, you know that there is
a mistake and you can then locate the error, correct it, and suddenly it makes sense.” So, the logical structure and the search for the one answer worked as a guidance of right and wrong.
Doing assignments played another role, namely, to be able to move on and build on top. In this way doing assignments became a step to learn further. Emma described how this one answer was used to either conclude something or to move further in logical thinking. Maja described how in lower secondary they would always get things explained several times so that all understood it properly. While in upper secondary they would learn new things almost every lesson and “build on top, on top, and on top”. She underlined the point by adding “this is why people often say that in mathematics you have to keep up”. Another young woman Clara explained how she often felt that she had acquired new knowledge “or better knowledge, that can reinforce what I knew already”. So, performing in mathematics was not only about assignments but also being able to learn hierarchically.
All 33 young women shared narratives containing interest in mathematics. This was expressed in different ways and often intertwined with affect. Most of the young women expressed interest in relation to their competences and their performances. How they liked doing mathematics in a specific way or being able to think in a specific way. For example, Lea who really liked the logic in mathematics and that there would always be a reason for the choices made. Another young woman Agnes highlighted writing all the different notations as really exciting. General interest in the subject was also expressed. For example:
Lara: I’m really interested in the subject…and when you pay attention in class it becomes more and more interesting, and you understand the homework and it just feels good.
And Astrid talked about mathematics as a language in itself and added:
Astrid: When you understand [mathematics]…then it just keeps being exciting because…biotechnology and physics, it does not make sense without mathematics. It’s like [mathematics] opens the door to other things in the world.
Both Lara and Astrid expressed how interest in mathematics would generate more interest in the subject as the understanding of the subject would become deeper and deeper. As such, understanding of the subject would go hand in hand with the interest in the subject. Astrid explained further that mathematics was fundamental for everything else. So, for her the interest in mathematics was supported by an idea about mathematics being essential to science subjects.
Recognition was likewise connected to their competences and performances. As the competences would present themself explicitly in the mind as a proof of something done correct. This self-awareness was by some expressed as leaving math-lessons aware of having acquired new knowledge. In relation to performances, many of the young women narrated that finding the correct answer was performing properly. This explicit way of being able to recognize oneself was likewise expressed in contrast to performing in other subjects. In subjects like Danish or social science expectations were unclear and therefore not as easy to perform properly. For example, Selda, contrasted performing in mathematics with performing in Danish. She explained “[In Danish] you have to analyze and constantly argue why it’s right” so performing in Danish was more unclear and complex, and therefore more difficult to be recognized within both by oneself but also by others. This contrast in being recognized in other subjects was expressed by several others. Sara made a comparison between mathematics and social science classes:
Sara: …in social science…it’s like ’if you mean that’ you are right and ‘if you mean this’ you are also right, and everything can be right in their own way…Where in mathematics…there is one answer.
So, the fuzziness of social science was contrasted to the exactness in mathematics. As such, expectations in mathematics were expressed as being crystal-clear and easier to act on. Another young woman Alma explained that the one answer in mathematics made her feel certain, especially compared to Danish and social science that she described as more uncertain subjects because “you try but you don’t know if it is correct anyway, because there exists no completely correct answer”. Again, the contrast between fuzziness and exactness were pointed out as a contrast between expectations and ways to perform. So, the existence of the one answer acted as a certainty and finding this one answer confirmed that it was done properly. Recognition by others could also be acquired when standing at the board going through a proof or a correct assignment or by handing in correct papers. Recognition was thereby centered around performing correct answers.
The young women ascribed different meanings to their experiences with upper secondary school mathematics. Some struggled with performing the math-identity while others saw themselves succeeding as either effortful or as having an ability. For the group that experienced performing their math-identities as troublesome performing entailed for example a feeling of not being ‘ready in the mind’ especially when arriving from another lesson. Some found it challenging to adjust themselves to the significant change of theoretical and abstract mathematics they were presented with in upper secondary school. The idea of mathematics being an individual process of getting the pieces in the puzzle connected was experienced as entailing additional effort at home. Amalie for example explained how she would have to look at it at home or else it would not be possible to follow the next lesson. Another group of the young women saw themselves as hard working and succeeding by being effortful. They perceived the logical sense-making of mathematics as something one could be able to do by putting in hard work. For example, Sara explained how she had always liked mathematics but sometimes found it challenging to remember all the rules and formulas. Lara expressed how she really liked mathematics and found it interesting but that she often was challenged. They both continued expressing that they resolved it, which made them feel successful. Others described learning new mathematics as something that had to be difficult otherwise one would not learn something new. Thus, for the young women in this group succeeding in mathematics implied being effortful and putting in hard work. The last group described learning mathematics as an innate or inherent ability, and thereby succeeding as easy and effortless. For example, Liva who found mathematics easy and described herself as having a math-brain, that only worked with concrete answers. Others described mathematics as effortless because they were either a math-nerd and considered themselves as one of the boys or because being good at mathematics was running in the family. Maja expressed that mathematics had always been easy for her as opposed to being dyslexic, thus contrasting the easiness of mathematics with a lack of ability.
In the following section the findings will be discussed.
Discussion/Conclusion
The aim of this paper was to explore how the construction of math-identities were shaped and constructed by successful female students in their meeting with upper secondary school mathematics. This was done by analyzing qualitative individual interviews with 33 young women. The thematic analysis showed how their identities were centered around an intuitively understanding and logical thinking not including playfulness and creativity. Also, a celebration of individualism was highlighted as well as the search for the correct answer through procedural methods while keeping strict attention to the hierarchy learning. This experience of mathematics to be rigid and inflexible is consistent with Boaler et al. (2000) however in this study the rigidness and inflexibility was highlighted as a positive aspect of mathematics.
The findings are interesting in at least two respects. First, because the young women’s narratives portray a specific and narrow route to identify with mathematics centered around an exactness. This celebrates and reproduces the idea of mathematics as for the ones that can perform correct answers. As a consequence, the room for discursive space is limited as one is either mathematical or not depending on the production of the correct answer. Second, because they showed variation among the young women in how they were able to see themselves and be seen by others in mathematics. This include performances that have been characterized as feminine (effortful and hardworking) as well as masculine (effortless and innate) (Mendick, 2006). These differences within the group of young women offers a broader understanding of successful young women’s identification with mathematics. Furthermore, this variation provide foundation for seeing beyond the body and move away from categorizing in sex/gender differences. Instead exploring differences that exist within what is categorized as boy/men and girl/woman as well as similarities between (Jaremus, 2021).
An additional perspective to explore in relation to this paper would entail the young women’s identities in relation to their background, to provide an understanding of how other axes of ethnicity, race, and class intersect with math-identity and gender. As middle-class girls tent to have more opportunities to create identities that align with fields, such as science and mathematics, that has been characterized as masculine (Archer and DeWitt 2015). Another perspective would focus on the young women’s emotions and the connection to their math-identities. As emotions and affective factors are an important part of understanding identification with mathematics (Bishop 2012). Further perspectives on the study as a whole would entail how the young women’s math-identities develop during their education. This approach is suggested by Anderson et al. (2015) to broaden the understanding of shifts in students’ identification with mathematics.
References
Andersson, A., Valero, P. & Meaney, T. (2015). “I am [not always] a maths hater”: Shifting students’ identity narratives in context. Educ Stud Math 90, 143–161. https://doi.org/10.1007/s10649-015-9617-z
Andrews, M., Squire, C., & Tamboukou, M. (2008). Doing narrative research. London: Sage.
Archer, L., & DeWitt, J. (2015). Science aspirations and gender identity: Lessons from the ASPIRES project. In E. Henriksen, J. Dillon, & J. Ryder (Eds.), Understanding student participation and choice in science and technology education (pp. 89–102). Dordrecht: Springer.
Bishop, J. P. (2012). “She’s always been the smart one. I’ve always been the dumb one”: Identities in the mathematics classroom. Journal for Research in Mathematics Education, 43(1), 34–74.
Boaler, J., & Greeno, J. G. (2000). Identity, agency, and knowing in mathematics worlds. In J. Boaler (Ed.), Multiple perspectives on mathematics teaching and learning (pp. 171–200). Westport: Ablex.
Boaler, Jo; Wiliam, Dylan; Zevenbergen, Robyn. (2000). The Construction of Identity in Secondary Mathematics Education. Paper presented at the International Mathematics Education and Society Conference (2nd, Montechoro, Portugal).
Braun, V., & Clarke, V. (2006). Using thematic analysis in psychology. Qualitative Research in Psychology, 3, 77–101.
Butler, J. P. (1990). Gender trouble: Feminism and the subversion of identity. London: Routledge.
Cass, C., Hazari, Z., Cribbs, J., Sadler, P., & Sonnert, G. (2011). Examining the impact of mathematics identity on the choice of engineering careers for male and female students. In Frontiers in Education Conference.
Carlone, H. B., & Johnson, A. (2007). Understanding the Science Experiences of Successful Women of Color: Science Identity as an Analytic Lens. Journal of Research in Science Teaching, 44(8), 1187-121
Darragh, L. (2016). Identity research in mathematics education. Educational Studies in Mathematics, 93(1), 19–33. https ://doi.org/10.1007/s1064 9-016-9696-5.
DE 2019: https://www.danskerhverv.dk/siteassets/mediafolder/dokumenter/13- pressemeddelelser/pigerne-er-bedst-til-matematik-igymnasiet---analyse.pdf
DES 2016: The Danish Education System. The Ministry of Higher Education and Science, The Ministry for Children, Education and Gender Equality and The Ministry of Culture. https://ufm.dk/publikationer/2016/the-danish-education-system
Flyvbjerg, B. (2011). Case study. In N.K. Denzin & Y.S. Lincoln (Eds.), The Sage handbook of qualitative research (4thed., pp. 301–316). Thousand Oaks, CA: Thousand Oaks.
Gee, J. P. (1999). An introduction to discourse analysis: Theory and method. Routledge.
Gee, J. P. (2000). Identity as an analytic lens for research in education. Review of Research in Education, 25, 99–125. https://doi.org/10.2307/1167322
GL 2020: https://www.gl.org/detmenergl/Sider/Ligestillingmellem-koennene-i- gymnasieuddannelserne.aspx
GL 2021:
https://www.gl.org/nyt/Documents/Søgetal%20til%20de%20gymnasiale%20uddannelser%202021%2 0overblik.pdf
Jaremus, F. (2021). When girls do masculinity like boys do: establishing gender heteroglossia in school mathematics participation. Math Ed Res J 33, 713–731. https://doi.org/10.1007/s13394-020-00355-6
Kvale, S. and S. Brinkmann (2009). Interview: introduktion til et håndværk, Hans Reitzel.
Mendick, H. (2005). A Beautiful Myth? The Gendering of Being/Doing "Good at Maths". Gender and Education, 17(2), 203-219.
Mendick, H. (2006). Masculinities in Mathematics. Educating Boys, Learning Gender. London: Open University Press.
Radovic, D., Black, L., Williams, J., & Salas, C. (2018). Towards Conceptual Coherence in the Research on Mathematics Learner Identity: a Systematic Review of the Literature. Educational Studies in Mathematics, 99(1), 21-42. https://doi.org/10.1007/s10649-018-9819-2
Radovic, D. Black, L. Sales, C.E., Williams, J. (2017). Being a Girl Mathematician: Diversity of Positive Mathematical Identities in a Secondary Classroom. Journal for Research in Mathematics Education, Vol. 48, No. 4, pp. 434-464.
Social Progress Index 2022: https://www.socialprogress.org/
UNESCO 2017: United Nations Educational, Scientific and Cultural Organisation. Cracking the code: girls’ and women’s education in science, technology, engineering and mathematics. Paris: Author. https://unesdoc.unesco.org/ark:/48223/pf0000253479
UVM 2022: https://www.uvm.dk/aktuelt/nyheder/uvm/2022/sep/220921-ekspertgruppe-er-klar-med- anbefalinger-til-at-styrke-matematikfaget